Last week, figures from the Reserve Bank of Australia showed home loan credit growth was at its lowest level ever recorded, with RBA records dating back to the 1970’s.
On Tuesday the ABS released the latest quarterly update to 6416.0, House Price Indexes: Eight Capital Cities, Jun 2011.
With extremely poor credit growth for housing, there was no surprise to see continued falls in house prices around the country, as Australia suffers from crippling levels of household debt and the unwinding of the First Home Owners Boost.
A reader has asked if we can update the Real House Price graphs, and with the ABS figures hot of the press it was the perfect time to do so. Our last update was in 2008, and it was scary then.
With our housing bubble once again faltering and GFC2 in kicking distance, we are seeing a surge of newcomers to this site. In this context, we will cover some existing ground and explain what real home prices are.
Real Home prices are simply prices (or an index) corrected for inflation. The U.S. is probably a great example, I’ll show this first :
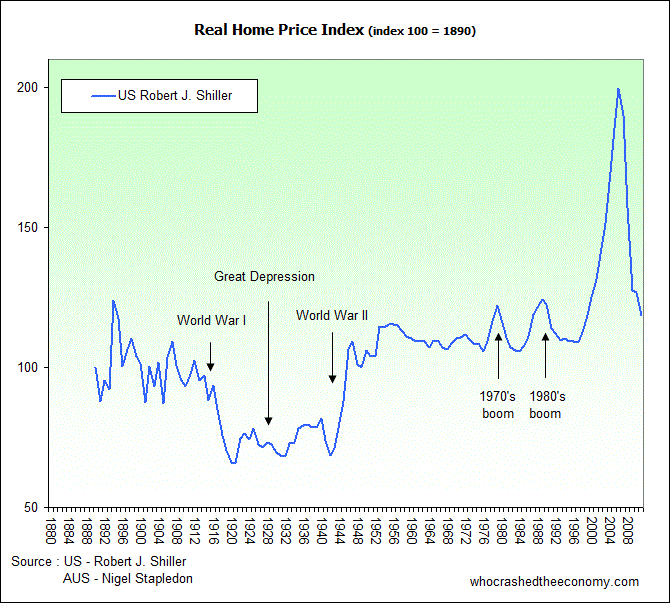
In this case, the index started in 1890 at 100 and tracks house prices, corrected for inflation and relative to 1890. What you will notice, is the index is relatively flat, that is, house prices today in the USA (after a huge bubble last decade) is not much more than in 1880, in today’s buying power. Assuming wages also tracked inflation, this means an American’s great grand parents paid roughly the same for a house in 1890 than today as a percentage of their income.
But as you can see, it wasn’t always like that. Easy credit and a real estate industry promoting ‘facts’ that house prices double every 7 years and a chronic shortage of homes caused a substantial housing bubble last decade, and when households couldn’t borrow any more to keep the ponzi scheme going, it imploded inwards causing GFC1. This is a good example that ‘a permanently high plateau’ (real estate professional speak) isn’t sustainable.
The data source for U.S. home prices comes from Robert J. Shiller, Professor of Economics at Yale University who wrote the book Irrational Exuberance. He frequently updates the U.S. data and posts it on http://www.irrationalexuberance.com
Now lets turn to Australian real home prices :
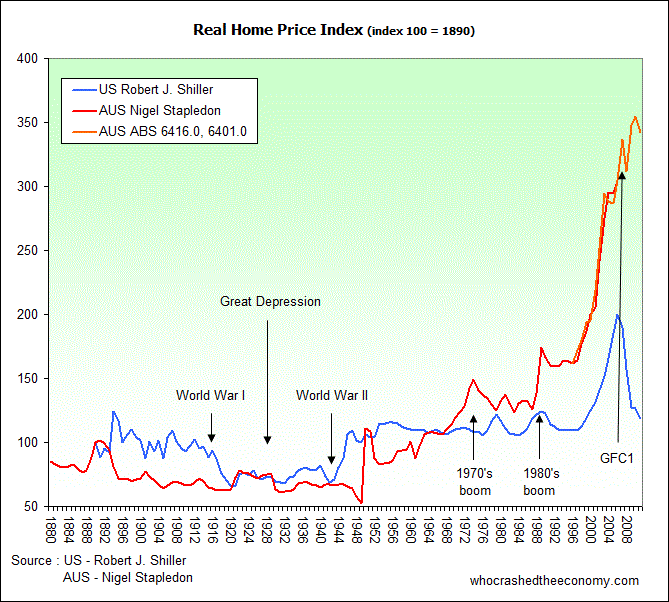
Yes, that’s America’s “little” bubble – the blue line down the bottom!
Our bubble continues to aim for the sky thanks to tax incentives such as negative gearing and what seems like bottomless stimulus. You will see a small decline during GFC1 before the Rudd Government introduced the First Home Owners Boost. According to Treasury Minutes, “The short term stimulus [BOOST] was designed to encourage people who had already been saving for a home to bring forward their purchase and prevent the collapse of the housing market.” This may of achieved the government’s short term goal and prevented the collapse of housing bubble in 2008, but it begs the question what is the government’s plans now that the BOOST has finished, and housing is once again falling?
The dataset for Australia comes from two sources. The majority of the data (1880 to 2006) comes from Dr Nigel Stapledon from the University of New South Wales. Prior to 2003, Dr Stapleton was Chief Economist for Westpac Bank. This dataset is continued (orange line) using data from the ABS.

I have just printed off the graph for my office wall to remind myself why I am delaying buying a house to live in. Thanks!
BTW would love to hear any opinions about how long a ‘correction’ would take to start in earnest. It seems to be gathering pace rapidly at the moment.
“Yes, that
I love the term GFC1 as it implies that there is second one coming 🙂
WOW just Wow. the top is definitely in. and it’s clearly a long way to any notion of fair value. with no prospects of targeted stimulus in housing this “investment” is done.
glad I have savings and secure (non cyclical) employment.
anyone hazard a guess: time to the bottom?
In answer to your question, I’d say the Govt is cooking up “Ponzi Stimulus FHVB Mark II”. The real question is whether the sheeple will kick up a stink about it or will they be put to sleep by Real-Estate prostitute … the MSM?
Ignorance is bliss.
Peter, I was actually considering adding GFC2 to the graph. My definition, GFC2 is the crisis that occurs after the stimulus of GFC1 wears off. In Australia’s case, we have now seen two quarters of falling house prices after the ceasing of the First Home Owners Boost. Therefore the downturn at the end of the graph is GFC2.
With China hiking rates and slowing down the commoditiy bubble is about to pop. When that happens you see inflation drop dramatically, unemployement will pick up and rates will drop like they did in 2008. Imagine what that will do to the housing market. The debt will shift from the people to the Aussie govt becaue the govt will have to bail out the banks. Everything I am reading says these short sellers are circling the Aussie banks something fierce because they smell trouble. When this happens then Australia will be in same s#$t that US, Europe and the rest of the world are in. China is already losing some major ground. Watch their GDP take a nose dive soon. What goes up must come down the same way as it did up. There is nothing special about the China or Australia economy.
I think people are just beginning to realise that the Australian economy is akin to the
Titanic ship in an upright position before it sinks into the ocean.
Therefore, Its time to do two things
[1] Place you seat in a vertical position
[2] Prepare for take off
Interesting comment Paddy. I certainly agree with you (I assume you mean that there will be a bail out?) and AverageBloke. The issue here is the government still has access to a printing press; I can almost guarantee there will be either another $900 cheque in the mail or some obscene bail-out for the financial institutions or another ridiculous grant of some sort. I hope all continues to plan since I shorted XDJ about a month ago (and it’s doing quite nicley!).
I have just sold an ‘investment property’ and boy am I glad to be out. I was sold down the track of or should I say spruiked down the track of the importance of property invesment for the future. What a sham. After 3 years of owning I came out with $10k in my pocket + the minor tax relief that I aquired with the headache of being a landlord which is all money I could have quite easily saved.
10k is not alot of money but when I found out the place had sold I felt as though I had won the lottery. They say the market is a little flat at the moment, however I peaked over the edge of that little ‘flat’ orange peak line shown above and geez that’s a long, long way down. So I have happily taken the lift and I will see you all at the bottom with my renting buddies posting a smile from ear to ear.
well my last $900 bought an oz of gold, this next stim will need to be $1600 to match it.
@ Jamie.
I am with you. My IP settles next week!
Your back… where have you been?
Pleased your back and posting. 🙂
Couple of things the Yanks call this the Great Recession, which I think is apt.
Also, Steve Keen re-branded the First Home Buyers Grant as the First Home Vendors Boost (I am suure you know) bit I think is damn accurate.
And as I am in a channeling mood I think I will channel some Paul Keating, “This is the recession Australia forgot to have but the markets did not!”.
Ouch.
My only questions now is do I turn my cash to gold and wait for the Australian Banking system to implode.
We all know the Aussie House Market is a dead man walking!
Eeek.
TM.
Australia is simply a bigger version of Ireland….lots and lots of debt offered via lose lending practices to Australians so that they could buy over inflated properties off each other, or create ‘investment portfolios’ on the premise that prices always go up and getting rich requires zero effort. The house price income ratio used has been misleading as it is based on total household income – recalculate it using a single income and the house price to income ratio is really scary and supports graphs in terms of the extent of the debt.
And with all that mining investment about to come on line……. Our resources are going to plummet in value. As a nation we couldn’t even handle a wine glut!
The stock market is rigged, and the IMF debt trap is just about to close on us.
Read ‘Confessions of an economic Hitman’ by John Perkins or look him up on youtube.
The easiest way for these multinational corporations and shady white shoe boy entities, to make endless money and gain endless power, is to send a country into massive debt, implode it, and then tell the country it has to sell off all it’s public assets for peanuts. South America has a lot of examples (pinocet anyone?)
Greece is the perfect example. Aided and abbetted by Goldman Sacks (of Shite) they hid Greeces financial situation and let them join the European Union. The hedge funds then shorted Greek bonds etc, and the ratings agencies (if you can’t see how corrupt these bastards are after the Lehmann – housing crises, you have your head up the ostriches bum that has its head in the sand) downgrade the nations rating so that they have no way out…..
…..EXCEPT – do as Iceland did…..Tell the IMF, the bankers and the hedge funds to go F*&^K themselves. Also, don’t believe what our government says. They are just as brainwashed and corrupted as Bush, Cheyney and Obama and 95% of economist out there. They will lead us down the same path given the smallest oppurtunity.
I appreciate your graph but I think you should use a logarithmic scale rather than linear. It more correctly reflects relatives movements in indexes. A linear scale exaggerates the movements in the top half of the graph relative to the bottom half.
I agree with your argument but I think that this is misrepresenting the facts and looks unprofessional.
Cheers
@Kirk. I think you will find these are ‘real’ house prices and are corrected for inflation. They are not suppose to go up exponentially, hence you don’t plot them on a log scale (unless you are a ‘unprofessional’ real estate economist!)
Here is one indexed at 1960 :
http://www.macrobusiness.com.au/wp-content/uploads/2011/08/ScreenHunter_10-Aug.-17-22.39.gif
Or one from the Treasury to 2004 :
http://www.treasury.gov.au/documents/939/images/abe_speech-5.gif (It was a bubble back then!)
Or another one from Alan Kohler :
http://t0.gstatic.com/images?q=tbn:ANd9GcQw6PkTS-KXdsexocOyQ19YxtsAp2oYJ_-sbTv9Usje-P4665hRbA
Woww that is phenomenal!
There is going to be a LOT of pain.
I don’t think all the stimulus in the world is going to save our bubble. The real problem is everyone has had enough debt. Sentiment has turned, and banks just can’t peddle their debt to us any more.
Those that were comfortable getting hocked up to the eyeballs have done so. Demand has been brought forward. Those that are left are the ones more cautious and uncomfortable with massive debts.
The banks need to launch a media blitz about the wonders and benefits of getting into as much debt as possible as quickly as possible to try and win these cautious people over.
They could title it “Borrowing your way to untold riches: All of the fun with none of the work”.
2 speed economy could have a 2 speed stimulus. A housing boost AND a Carbon tax.
But hey think outside the square. a baby bonus, have a baby get a free house.
it is just silly enough to be possible
When will it all end? Whom knows.. I think it will be a slow decline rather than an abrupt crash of property prices. Nearly 4 years in and property prices in USA are still in decline, I would expect a similiar situation here in Australia.. maybe 5 or 6 years of decline… some areas will be less impacted than others and may nearly stagnate. I have friends that live in the US and where they are prices have not “dropped” but have held 2007 prices I saw when I was there then.. Adjusted for inflation they have dropped but the “sticker” prices are the same, what was $250k then is still $250K now..